


Next: Exercice 17
Up: Index
Previous: Exercice 15
a) Montrer que
est une bijection de
 dans
dans
 .
.
b) On pose  et
et  . Exprimer
. Exprimer  et
et  en fonction de
en fonction de  et
et  et inversement.
et inversement.
c) Soient
et
Démontrer que la restriction de 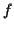 à
à  est une bijection de
est une bijection de  sur
sur
 .
.
Thème(s) : Nombres complexes
Non corrigé.